EECS 31/CSE 31/ICS 151 Homework 2 Questions with Solutions

View Questions Only
View Questions with Strategies

Problem 1

Question

(Theorems of Boolean algebra) Give proofs to the following theorems.

  1. Theorem 3(a) and (b)
  2. Theorem 6(a) and (b)

Solution

  1. Theorem 3(a) and (b)

    THEOREM 3(a) Law of Absorption : yx+x = x.

    Proof :

     yx+x = yx+x1        by identity (Ax. 2b)
      = x(y+1)       by distributivity (Ax. 4a)
      = x1           by Theorem 2(a)
      = x            by identity (Ax. 2b)

    THEOREM 3(b): x(x+y) = x by duality.

  2. Theorem 6(a) and (b)

    THEOREM 6(a) De Morgan's Laws: (x+y)' = x'y'.

    Proof: We will prove that x'y' is a complement of x+y by proving that x'y' satisfies Axiom 5, which states that x+x' = 1 and that xx' = 0. Thus we have to prove that (a) (x+y)+(x'y')=1 and (b) (x+y)(x'y') = 0.

    Part (a):

     (x+y)+(x'y') = x+(y+(x'y'))        by assiociativity (Th. 5a)
              = x+((x'y')+y')       by commutativity (Ax. 3a)
              = (x+(x'y'))+y        by assiociativity (Th. 5a)
              = (x+x')(x+y')+y      by distributivity (Ax. 4b)
              = 1(x+y')+y           by complement (Ax. 5a)
              = (x+y')+y            by identity (Ax. 2b)
              = x+(y'+y)            by assiociativity (Th. 5a)
              = x+1                 by complement(Ax. 5a)
              = 1                   by Theorem 2(b)

    Part (b):

     (x+y)(x'y') = x(x'y')+y(x'y')      by distributivity (Ax. 4a)
             = x(x'y')+y(y'x')      by commutativity (Ax. 3b)
             = (xx')y'+(yy')x'      by associativity (Th. 3b)
             = 0y'+0x'              by complement(Ax. 5b)
             = 0+0                  by identity(Ax. 2b)
             = 0

    THEOREM 6(b): (xy)' = x'+y' by duality.

Problem 2

Question

(Theorems and proofs) Using truth tables, prove the validity of the following identies.

  1. (xyz)' = x'+y'+z'

Solution

x y z (xyz)' x' y' z' x'+y'+z'
0 0 0 1 1 1 1 1
0 0 1 1 1 1 0 1
0 1 0 1 1 0 1 1
0 1 1 1 1 0 0 1
1 0 0 1 0 1 1 1
1 0 1 1 0 1 0 1
1 1 0 1 0 0 1 1
1 1 1 0 0 0 0 0

Problem 3

Question

(Boolean functions) Derive truth tables for the following Boolean functions.

  1. F(x, y, z) = (x+z)'
  2. F(x, y, z) = (x+z)'(x+y')

Solution

  1. F(x, y, z) = (x+z)'
    x y z x+z (x+z)'
    0 0 0 0 1
    0 0 1 1 0
    0 1 0 0 1
    0 1 1 1 0
    1 0 0 1 0
    1 0 1 1 0
    1 1 0 1 0
    1 1 1 1 0
  2. F(x, y, z) = (x+z)'(x+y')
    x y z (xyz)' x+y' (x+z)'(x+y')
    0 0 0 1 1 1
    0 0 1 0 1 0
    0 1 0 1 0 0
    0 1 1 0 0 0
    1 0 0 0 1 0
    1 0 1 0 1 0
    1 1 0 0 1 0
    1 1 1 0 1 0

Problem 4

Question

(Boolean algebra) Prove by algebraic manipulation that the following expressions are equivalent.

  1. x'y'+xy = (xy'+x'y)'
  2. x'z+xy = x'y'z+yz+xy

Solution

  1.  (xy'+x'y)' = (xy')'(x'y)'                 De Morgan's
            = (x'+y)(x+y')                 De Morgan's
            = x'x+x'y'+xy+yy'              distributivity
            = x'y'+xy                      identity 


  2.  x'z+xy = x'z+xy+xy                        idempotency
        = x'z(y+y')+xy(z+z')+xy            identity
        = x'yz+x'y'z+xyz+xyz'+xy           distributivity
        = x'y'z+(x+x')yz+xy                distributivity
        = x'y'z+yz+xy                      identity

Problem 5

Question

(Algebraic manipulation) Minimize the number of operators in the following Boolean expressions.

  1. x'y'+xy+xy'
  2. (x+y)(x+y')

Solution

  1. x+y'
  2. x

Problem 6

Question

(Boolean implementations) Implement the XOR function by means of:

  1. NAND gates only
  2. NOR gates only
  3. AND, OR, and NOT gates

Solution

Problem 6 Solution

Problem 7

Question

(Boolean implementations) Implement x XOR y XOR z using the components in the basic logic library presented in Table 3.14. Find the implementation that has:

  1. The smallest cost
  2. The shortest delay

Solution

Notice that XNOR has the smallest delay. Therefore, we first try using the XNOR implementation.

 F = x XOR y XOR z
   = (x XOR y)z' + (x XOR y)'z                      by definition of XOR
   = (xy' + x'y)z' + (xy' + x'y)'z                  by definition of XOR
   = xy'z' + x'yz' + (xy' + x'y)'z                  by distributivity
   = xy'z' + x'yz' + (x' + y)(x + y')z              by De Morgan's law
   = xy'z' + x'yz' + (x'x + x'y' + xy + yy')z       by distributivity
   = xy'z' + x'yz' + (x'y' + xy)z                   by complement
   = xy'z' + x'yz' + x'y'z + xyz                    by distributivity
   = (xy' + x'y)z' + (x'y' + xy)z                   by distributivity
   = (xy + x'y')'z' + (x'y' + xy)z                  by complement
   = x XNOR y XNOR z                                by definition of XNOR

The solutions for (a), (b) and (c) are the same:

Problem 7 Solution 
 Cost  = 12 + 12   = 24
 Delay = 3.2 + 3.2 = 6.4

Problem 8

Question

(Logic Libraries) Using the basic logic library presented in Table3.14, implement the full subtractor that is specified by the following table:

   Xi   Yi   Bi |   Bi+1    Di
 ------------------------------
   0    0    0  |    0      0
   0    0    1  |    1      1
   0    1    0  |    1      1
   0    1    1  |    1      0
   1    0    0  |    0      1
   1    0    1  |    0      0
   1    1    0  |    0      0
   1    1    1  |    1      1

Find the implementation that has:

  1. The smallest cost
  2. The shortest delay

Solution

  1. The smallest cost using NAND gates

     Bi+1 = x'y'b + x'yb' + x'yb + xyb          by definition
      = x'(y'b + yb') + yb(x'+x)            by distributivity
      = x'(y'b + yb') + yb                  by complement
      = x'((y'b)' (yb')')' + yb             by De Morgan's law
      = ((x' ((y'b)' (yb')')')' (yb)' )'    by De Morgan's law

 Di = x'y'b + x'yb' + xy'b' + xyb                       by definition
    = x'(y'b + yb') + x(yb + y'b')                      by distributivity
    = x'((y'b)'(yb')')' + x((yb')(y'b')')'              by De Morgan's law
    = ((x'((y'b)' (yb')')')' (x((yb') (y'b')')')')'     by De Morgan's law
    smallest cost using NAND gates figure 
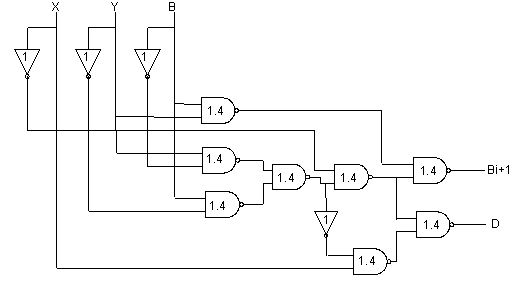
     Cost  = 4 x 8 + 2 x 4   = 40
 Delay = 1 x 2 + 1.4 x 4 = 7.6

  2. The shortest delay

     Bi+1 = x'y'b + x'yb' + x'yb + xyb           by definition
      = b(xy + x'y') + x'y(b'+b)             by distributivity
      = (b((xy)' (x'y')' )' + x'y            by complement
      = ((b((xy)' (x'y')')')' (x'y)')'       by De Morgan's law

 Di = x'y'b + x'yb' + xy'b' + xyb                       by definition
    = x'(x'y + xy') + b(xy + x'y')                      by distributivity
    = b'((x'y)'(xy'))' + b((xy)'(x'y')')'               by De Morgan's law
    = ((b'((x'y)' (xy'))')' (b((xy)' (x'y')')')' )'     by De Morgan's law
    shortest delay figure 
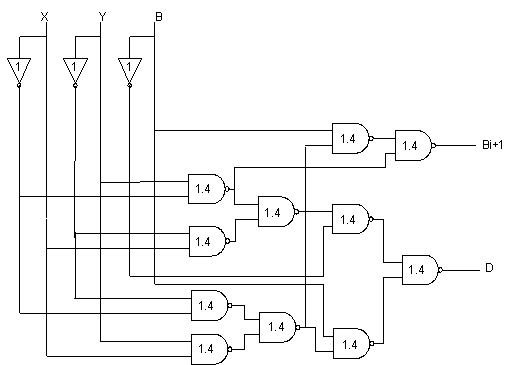
     Cost = 2 x 3 + 4 x 11 = 50
 Delay = 1 + 1.4 x 4   = 6.6

Problem 9

Question

(Logic Libraries) Redo Problem 3.15 using only the gates that are given in Table 3.15 and 3.16

Solution

  1. The smallest cost 
     F = (xy' + x'y)z' + (xy' + x'y)'z 	        by XOR definition
   = ((xy' + x'y)' + z)' + (xy' + x'y)'z 	by De Morgan's law

    Smallest Cost Figure

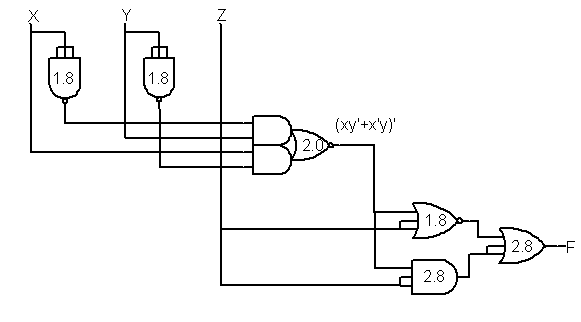
     Cost  = 6x8                   = 48
 Delay = 1.8 + 2.0 + 2.8 + 2.8 = 9.4
  2. The shortest delay and the smallest cost-delay product 
     F = xyz + x'y'z + x'yz' + xy'z'            by XOR definition
   = ((xyz + x'y'z + x'yz' + xy'z')')'      by involution
   = ((xyz)' (x'y'z)' (x'yz')' (xy'z')')'   by De Morgan's law
    Or 
     F = (x + y + z) (x + y' + z') (x' + y + z')(x' + y' + z)               by definition
   = (((x + y + z) (x + y' + z') (x' + y + z') (x' + y' + z))')'        by involution
   = ((x + y + z)' + (x + y' + z')' + (x' + y + z')' + (x' + y' + z)')' by De Morgan's law

    Shortest Delay and Smallest Cost Problem 9 Figure

     Cost         = 7 x 8+10        = 66
 Delay        = 1.8 + 1.8 + 2.2 = 5.8
 Cost x Delay = 382.8

Problem 10 (3.18)

Question

(Logic Libraries) Redo Problem 3.15 using any of the standard logic gates that are given in Table 3.14, 3.15 and 3.16

Solution

  1. The smallest cost and the smallest cost-delay product 
     F = x XOR y XOR z = x XNOR y XNOR z       by problem 3.15

    Smallest Cost and Smallest Cost-Delay Problem 10 Figure

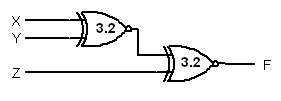
     Cost  = 2 x 12  = 24
 Delay = 2 x 3.2 = 6.4
 Cost x Delay = 153.6
  2. The shortest delay 
     F = ((xyz)' (x'y'z)' (x'yz')' (xy'z')')'  by problem 3.17

    Shortest Delay Problem 10 Figure

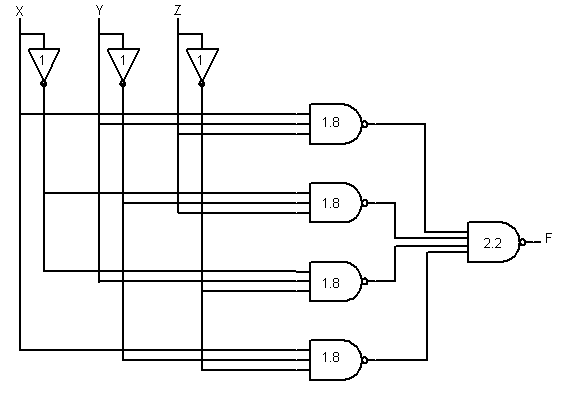
     Cost = 3 x 2 + 4 x 8 + 10 = 48
 Delay = 1.0 + 1.8 + 2.2   = 5.0 ns

Problem 11 (3.19)

Question

(Gate arrays) Using a 3-input NAND gates, derive a logic schematic of a:

  1. full adder
  2. full subtractor

Solution

  1. Full Adder
    1. Write the truth table for the full adder. 
        Xi   Yi   Ci |  Ci+1   Si
 -------------------------
  0    0    0  |  0     0
  0    0    1  |  0     1
  0    1    0  |  0     1
  0    1    1  |  1     0
  1    0    0  |  0     1
  1    0    1  |  1     0
  1    1    0  |  1     0
  1    1    1  |  1     1
    2. Write out sum of product expression of this truth table. 
      Ci+1 = Xi'YiCi + XiYi'Ci + XiYiCi' + XiYiCi
     = YiCi + XiCi + XiYi
Si   = Xi'Yi'Ci + Xi'YiCi' + XiYi'Ci' + XiYiCi
    3. Convert this expression into format with no more than 3 operator sub-expression or 3 literals. If the expressions contain more than 3 operators or literals, group them into 3-input operator. 
      Ci+1 = YiCi + XiCi + XiYi
     = (YiCi)' (XiCi)' (XiYi)')'
 Si  = Xi'Yi'Ci + Xi'YiCi' + XiYi'Ci' + XiYiCi
     = (((Xi'Yi'Ci)' (Xi'YiCi')' (XiYi'Ci')')'' (XiYiCi)')'
    4. Represent this two expression with 3-input NAND gates.

      Full Adder 3-input NAND gates Problem 11 Figure

       Cost = 6 x 14 = 84
 Delay: Input to Si   = 1.8 x 5 = 9.0
        Input to Ci+1 = 1.8 x 3 = 5.4
  2. Full Subtractor
    1. Write the truth table of full subtractor. 
        Xi  Yi  Bi   |  Bi+1 Di
 -------------------------
  0    0    0  |  0    0
  0    0    1  |  1    1
  0    1    0  |  1    1
  0    1    1  |  1    0
  1    0    0  |  0    1
  1    0    1  |  0    0
  1    1    0  |  0    0
  1    1    1  |  1    1
    2. Write out sum of product expression of this truth table. 
      Bi+1 = Xi'Yi'Bi + Xi'YiBi' + Xi'YiBi + XiYiBi
Di   = Xi'Yi'Bi + Xi'YiBi' + XiYi'Bi' + XiYiBi
    3. Convert this expression into format with no more than 3 operator sub-expression or 3 literals. If the expressions contain more than 3 operators or literals, group them into 3-input operator. 
      Bi+1 = Xi'Yi'Bi + Xi'YiBi' + Xi'YiBi + XiYiBi
     = (((Xi'Yi'Bi)' (Xi'YiBi')' (XiYiBi)')'' (Xi'YiBi)')'
 Di  = Xi'Yi'Bi + Xi'YiBi' + XiYi'Bi' + XiYiBi
     = (((Xi'Yi'Bi)' (Xi'YiBi')' (XiYiBi)')'' (XiYi'Bi')')'
    4. Represent this two expression with 3-input NAND gates.

      Full Subtractor 3-input NAND gates Problem 11 Figure

       Cost = 6 x 12 = 72
 Delay: Input to Di   = 1.8 x 5 = 9.0
        Input to Bi+1 = 1.8 x 5 = 9.0